Récit du débat autour de la création de Sambo

(1) Moi aussi j’ai envie de t’écrire. Ce qui sort de ton travail, c’est le silence du maître et le silence de l’enfant (Sambo). Plus que le silence, c’est l’abstention. Le maître souffre, il voudrait profiter du pouvoir que lui donne son savoir. mais il se réjouit du plaisir « politique » que lui donne sa capacité à se taire, politique parce que ce sont les gens de la base qui construisent leur savoir. La quasi inutilité de l’établissement, sous ta suggestion, de la table de Pythagore : ce n’était qu’une information. Ils l’ont faite, c’est une connaissance. « Connaître, c’est primairement computer. Computer, c’est opérer sur des signes, symboles, formes via signes, symboles, formes. » (Edgar Morin) Tu vois opérer !

(2) Ça, ça me plaît cette attitude de Sambo. Quand quelqu’un sera disponible, il pourra s’intéresser plus particulièrement aux différentes attitudes de ses enfants face à la création (nous avons ainsi une infinité de pistes de recherche dans notre pratique si neuve). Il y aurait aussi les sources de la création (psychanalytique ? événementielle, affective, multiples).

(3) Là, il y a une sorte d’imperfection : la structure n’est pas pure, mais elle est sous-jacente. C’est souvent ce qui nous émeut dans les dessins d’enfants. Ils ont voulu la structure mais ils l’ont heureusement manquée. Picasso a beaucoup exploré le gauchissement.

(4) Quel progrès tu as réalisé. voici ce que j’ai écrit à Jean Astier à ce sujet. « Mais vous posez aussi le problème de votre évolution personnelle qui est pour Monique un desserrement de sa peur, une confiance installée devant les résultats obtenus. Et c’est moi qui ai lancé ça, en m’interdisant d’avoir peur avant Noël. Et puis tu n’es pas un homme si tu n’as pas le courage d’aller jusqu’à Pâques ». Je sens qu’on va vers la confirmation d’ancien article : « Deux points c’est tout ». Que j’expérimente seul, aucune importance. Mais Monique expérimente aussi la non-peur. Et la non-peur peut se propager comme un mal qui répand la terreur. C’est ce que je souhaite pour l’humanité. Amen !

(5) Mais là tu interviens. Ce serait infiniment mieux si c’était venu d’un enfant (plus d’inscription dans la mémoire pour des raisons affectives). Mais le maître a le droit d’intervenir. Il ne faut pas être extrémiste. D’ailleurs les erreurs qu’il commet se réparent avec le temps (la dialectique de l’erreur du maître et de sa réparation).

(6) Oui, ça te coûte; toi, tu sais et tu te tais !!!

(7) Référence à une expérience antérieure qui peu à peu se trouve éclairée, ne serait-ce que par l’introduction du mot degré.

(8) Faut vraiment que tu sois motivée pour réussir à te taire à ce point. Mais tu es payée de ton effort. C’est peut-être ce plaisir que tu as découvert que tu cherches à retrouver.

(9) Non, il ne me semble pas que tu leur apprennes, tu leur fournis une information (le maître en a heureusement). Et elle peut être refusée ou acceptée, ça dépend si elle tombe juste au bon moment.

(10) Moi aussi j’attends la suite avec curiosité. S’il en reste quelque chose, comment se manifestera-t-il ? dans de nouvelles créations ? dans des interventions ? en dehors des maths ? dans une assurance acquise grâce à la reconnaissance de sa valeur ? pour le travail qu’il a su provoquer ?

Lorsque je me suis lancée dans la méthode naturelle de mathématique avec mes élèves suite à une participation à un atelier de Paul Le Bohec, j’ai pris l’habitude de lui envoyer régulièrement les comptes rendus de mes séances de débat autour des créations. Paul me les renvoyait annotés : il m’indiquait d’autres pistes que celles exploitées par les enfants, pas pour dire que c’était ce qu’il aurait fallu faire mais pour mettre le doigt sur tous les concepts mathématiques sous-jacents dans les créations des enfants. L’échange a duré deux années scolaires (1985 à 1987). L’année suivante, nous avons cessé nos échanges, j’étais suffisamment grande pour travailler seule ! Mais un jour j’ai tout de même eu envie de raconter une création à Paul (1), car j’étais satisfaite et de plus en plus persuadée que nous étions dans le vrai en pratiquant le débat mathématique libre autour des créations mathématiques des enfants.Voici colonne de droite mon compte rendu et colonne de gauche, les annotations de Paul.(24 mars 1988)

Au moment de mettre les créations au tableau, il manque le carnet de Sambo.
Sambo est le seul élève de la classe qui ne remplit pas son carnet à l’avance ( il ne fait d’ailleurs rien comme les autres, enfant en gros échec scolaire, perturbé, mal latéralisé, il bégaye… ).
Mais comme il aime qu’on travaille sur ses trouvailles, en vitesse, il griffonne quelque chose, création faite d’instinct, sans réflexion. (2) (elle est aussi mal faite que ça, faite en 2 secondes) (3) Je la mets donc au tableau en l’état.

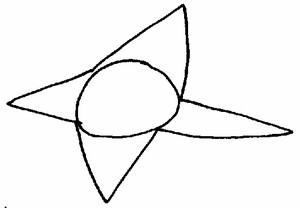
Commentaire des élèves :

- Il y a un rond.
- Non, c’est un cercle.
- Non, ce ne sont pas des triangles, le troisième côté n’est pas droit.
- Moi je vois un polygone qui a 8 côtés et au milieu un cercle.
- Et il y a des axes de symétrie.
- Oui, il y en a 4.

Moi, je me régale, je n’ai toujours rien dit, (ça j’ai appris à le faire) je suis ravie parce que les enfants me resservent des notions de géométrie acquises durant les mois précédents lors de nos séances de créations. Ce qui est dit, je ne l’ai pas provoqué, je sais donc qu’ils savent. (4)

- Les axes, on ne les voit pas bien parce que je trouve que c’est mal dessiné, il faudrait le refaire.

Accord général : Quand il s’agit de prendre règle et compas, c’est la joie générale, ils adorent dessiner au tableau.

- C’est sur le tableau quadrillé qu’il faut refaire la figure et sur le cahier en s’aidant des carreaux pour que ce soit plus facile.

Accord de tous. Un groupe fait au tableau, le reste sur les cahiers :

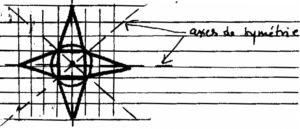
Tout le monde est ravi du résultat, content, admire alors moi j’interviens : « D’accord, c’est bien, la figure est belle et régulière, vous y êtes arrivés mais c’est grâce aux carreaux, mais si il n’y avait pas eu de quadrillage sur notre tableau ? » (5)

Alors ils me prennent au mot et se lancent dans la construction sur le tableau vierge.
Beaucoup de tâtonnement, des dessins à peu près qu’on efface ensuite après vérification (mesure). Alors quelqu’un a l’idée de dessiner les axes de symétrie pour s’aider. (Moi je ne propose rien, pourtant je sais comment il faut faire.) (6)
Pour les 2 premiers axes, pas de problème (le vertical et l’horizontal), ils sont tracés avec règle et équerre.

- Les 2 autres passent au milieu.
- Si c’est le milieu c’est la moitié de l’angle droit.
- C’est 90 et la moitié 45.

Ils annoncent ces nombres sans savoir ce que ça représente vraiment, mais ils ont fait avancer et tourner la tortue logo de l’ordinateur, ils savent que pour tourner droit, c’est 90 et la moitié 45. (7)
Un enfant prend la règle et essaie de trouver 90 et 45 mais ça ne marche pas, il tourne dans tous les sens sans succès.

- C’est normal, la règle c’est pour des longueurs, là, ce ne sont pas des longueurs, on tourne.

Un enfant prend l’équerre : échec, puis le compas, tâtonne, de nouveau échec.

- Il y a un autre instrument de géométrie qui n’a pas encore servi, on peut peut-être essayer.

Alors, moi je jubile, je ne dis toujours rien, je laisse faire et ils arrivent à placer le rapporteur, 0 sur un axe et 90 sur l’autre.(8)
Je leur apprends « degré » au passage, on regarde la différence entre la règle et le rapporteur.(9)
On finit la figure vite maintenant que les 4 axes sont tracés avec compas et règle.

Voilà pour la création de Sambo qui pendant toute la séance n’est pas intervenu mais a tourné autour de nous les mains dans les poches, semblant ne rien perdre de la démarche. Qu’en restera-t-il pour lui ? Je n’en sais rien, j’attends la suite. En tout cas, nous, nous nous sommes régalés et ce à partir d’un griffonnage fait en 2 secondes.(10)

Monique Quertier (2007)